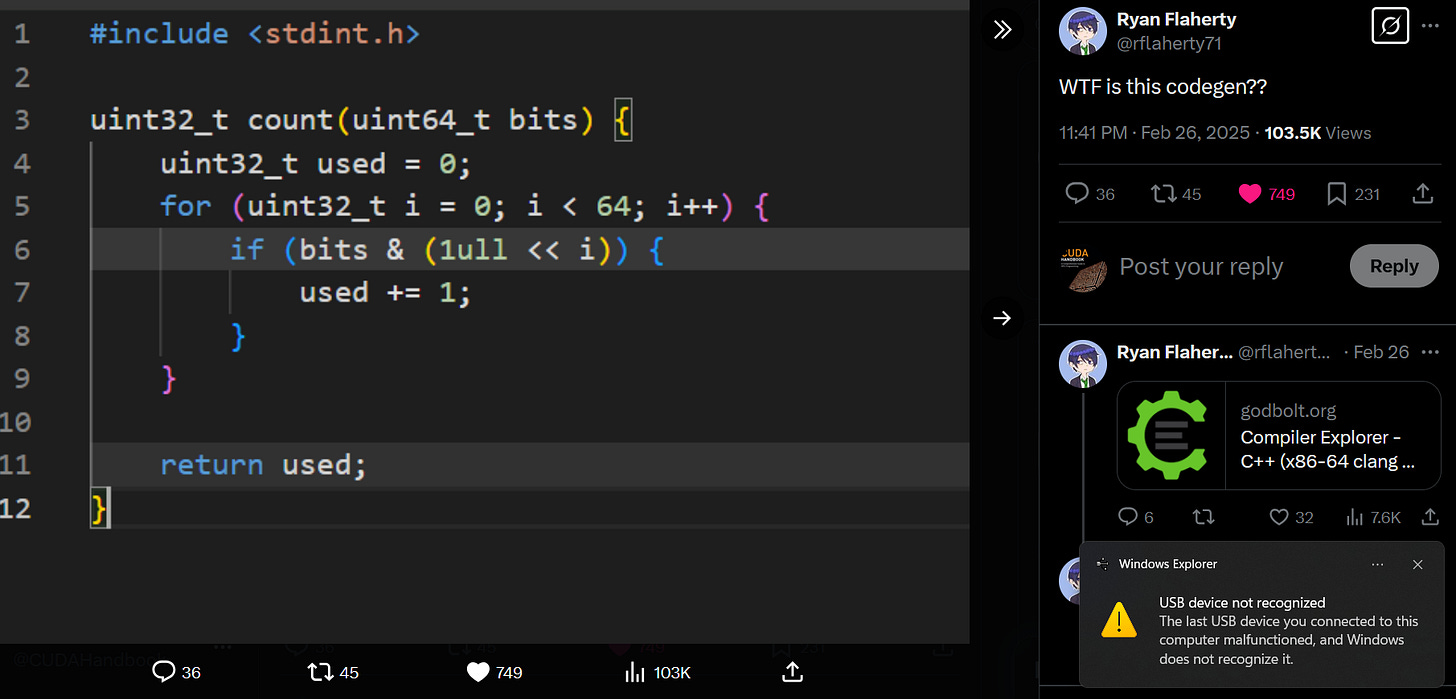
Given an integer, compute how many set bits it contains. How many thought cycles have been dedicated to optimizing this function?
Recently on Twitter, a code fragment was posted with the comment: “WTF is this codegen??”:
The code generated by clang, with the right optimization parameters, admittedly does look insane - here’s a fragment:
Why would the innocuous-looking function count generate machine code that looked like this?
It’s especially insane when you consider that the function implements a primitive operation known as the “population count” or “popcount,” which once was a popular coding interview question for candidates who had voiced an affinity for low-level programming. Let’s take a tour of a sampling of popcount implementations.
A Bevy Of Popcounts
The popcount implementation from the tweet seems designed to elicit bad code generation:
uint32_t
popcount_0( uint64_t x )
{
uint32_t ret = 0;
for ( uint32_t i = 0; i < 64; i++ ) {
if ( x & (1ull<<i) ) {
ret += 1;
}
}
return ret;
}This function is one of the least-optimized popcount implementations I’ve ever seen. To be honest, candidates who could write syntactically correct C code on a whiteboard were already in an elite class, so I wouldn’t say that the above-captioned implementation would be disqualifying; but a talk about how to make it faster surely would be warranted.
I am old enough to remember when it would’ve been a bit faster to shift the input right one bit, then conditionally increment the return value by executing an ADC (add with carry) instruction with an immediate 01. When each instruction costs several clock cycles, conserving the dynamic instruction count improves performance. Modern superscalar CPUs run that popcount implementation just as fast as more-readable ones, even if they are compiled into functions with more instructions.
Instead of computing a new mask value on each loop iteration (or relying on the compiler to create an induction variable and do the same thing), it is more common to at least sweep a mask variable across the input:
uint32_t
popcount_1( uint64_t x )
{
uint32_t ret = 0;
uint64_t mask = 1ull;
while ( mask ) {
if ( x & mask ) ret += 1;
mask <<= 1;
}
return ret;
}The compiler may emit fewer instructions since we are using the mask variable as a sentinel. The loop still iterates 64 times, however, so we can contrive to early-out of the function by e.g. repeatedly shifting the input value rightward until it becomes zero:
uint32_t
popcount_2( uint64_t x )
{
uint32_t ret = 0;
while ( x ) {
ret += x&1;
x >>= 1;
}
return ret;
}This implementation returns as soon as the least-significant set bits of the input have been counted. You can further improve on this optimization with a clever transformation, attributed by Knuth to Peter Wegner2, that clears the least significant set bit in a word: x &= x-1
uint32_t
popcount_3( uint64_t x )
{
uint32_t ret = 0;
while ( x ) {
ret += 1;
x &= x-1;
}
return ret;
}The loop in this function only iterates as many time as there are set bits in the input word. So pervasive is this transformation for bit-counting that g++ actually translates the above function into a POPCNT instruction!
Finally, the king of popcount implementations (absent hardware support; the POPCNT instruction was added to x86 along with SSE4.2), is a formulation exhaustively detailed in Hacker’s Delight. There are many, and you are invited to review them yourself. One representative example is as follows:
uint32_t
popcount_delight( uint64_t x )
{
x = (x & 0x5555555555555555ull) + ((x >> 1) & 0x5555555555555555ull);
x = (x & 0x3333333333333333ull) + ((x >> 2) & 0x3333333333333333ull);
x = (x & 0x0F0F0F0F0F0F0F0Full) + ((x >> 4) & 0x0F0F0F0F0F0F0F0Full);
x = (x & 0x00FF00FF00FF00FFull) + ((x >> 8) & 0x00FF00FF00FF00FFull);
x = (x & 0x0000FFFF0000FFFFull) + ((x >>16) & 0x0000FFFF0000FFFFull);
x = (x & 0x00000000FFFFFFFFull) + ((x >>32) & 0x00000000FFFFFFFFull);
return x;
}What the hell is going on here? This implementation considers each bit in the input to be its own population count; the mask of 0x5’s clears every other bit, and doing that operation to the input after shifting one bit to the right, lines up those 1-bit population counts so they can be added to each other to create thirty-two 2-bit lanes that each contain the population count of the corresponding 2-bit field within the input. The mask of 0x3’s and a 2-bit shift then is used to create sixteen 4-bit lanes that each contain the population count of the corresponding 4-bit field in the input. Consecutively doubling the width of the bit count eventually yields the result after lgk steps where k is the number of bits in the input.
Finally, we have the function that OP should’ve written in the first place: one that invokes the POPCNT instruction, available on x86 since 2008.
uint32_t
popcount_popcount( uint64_t x )
{
return _mm_popcnt_u64( (unsigned long long) x );
}Note that AVX512 includes vector POPCNT instructions that can compute the popcount of up to 16 or 8 32-bit and 64-bit operands in a single instruction, respectively.
What Was Going On With OP’s Popcount?
As I surmised after reflecting on it overnight, the original formulation - the one with 64 explicit loop iterations, that computes and recomputes the mask in the loop - is being vectorized by CLANG when -mavx2 is specified on the command line. Instead of a small loop of 4-6 instructions, it unrolls to more than 60 AVX2 instructions that use no fewer than 17 AVX2 (32-byte) global variables - a total of 578 bytes - to orchestrate the vectorization of the 64-iteration loop. The function performs surprisingly well in our contrived performance harness, but I think that’s mostly because the 578 bytes of globals are hot in the L1 cache, where they would be crowding out more important data in any workload that was doing something useful.
A Test/Performance Harness
Now that we have a bunch of popcount implementations to choose from, we can create a test harness to compare their performance. I wrote a simple program that computes the number of RDTSC clocks per iteration of a loop that processes a randomized set of integers. The popcount routine to test is given as a parameter.
auto clocks_per_popcount = []( uint32_t *out, const uint64_t *p,
size_t N, uint32_t(*pfn)(uint64_t) ) -> double
{
uint64_t start = __rdtsc();
for ( size_t i = 0; i < N; i++ ) {
out[i] = pfn( p[i] );
}
double et = (double) (__rdtsc() - start);
return et / N;
};The function that invokes this lambda, itself is a lambda invoked from the main function. It takes a gold array that contains the correct popcounts.
auto test_and_report_clocks = [clocks_per_popcount](
const std::string& name,
uint32_t *counts,
const uint64_t *in,
const uint32_t *counts_gold,
size_t N,
uint32_t(*pfn)(uint64_t) ) -> bool
{
memset( counts, 0, N*sizeof(counts[0]) );
(void) clocks_per_popcount( counts, in, N, pfn );
std::cout << name << ": ";
std::cout << clocks_per_popcount( counts, in, N, pfn ) << std::endl;
for ( size_t i = 0; i < N; i++ ) {
if ( counts[i] != counts_gold[i] ) {
std::cerr << "Popcount failed" << std::endl;
exit(1);
return false;
}
}
return true;
};Conclusion with Performance Results
You can look at the code and generated code on godbolt here.
Using g++ 9.4 with -O2, my laptop produces the following timings (remember, these are not clock cycles, just apples-to-apples comparisons of timestamp differences obtained from RDTSC):
popcount_0: 134.837
popcount_1: 68.0302
popcount_2: 72.4794
popcount_3: 70.3096
popcount_3a: 4.55477
popcount_delight: 8.67235
popcount_popcount: 4.51026The popcount_3/popcount_3a differences stem from g++ detecting that the Wegner optimization is being used to construct a popcount. Adding the volatile keyword forces the compiler to emit the loop code, which has performance similar to popcount_2. And of course, g++ does not vectorize popcount_0, the function that started all this trouble. Essentially, these g++ performance results illustrate why a candidate would get asked further questions if they wrote popcount_0 on the whiteboard.
Compiling with clang (with -O2 -mavx2), we can reproduce the code generation that prompted the original tweets, and measure the resulting performance:
popcount_0: 14.4106
popcount_1: 55.3924
popcount_2: 61.718
popcount_3: 72.2239
popcount_3a: 2.17638
popcount_delight: 2.74729
popcount_popcount: 2.08722The vectorized popcount_0 that generates all that unwelcome memory traffic runs surprisingly fast, more than 8x faster than the naive code emitted by g++.
As with g++, clang compiles the Wegner formulation into a POPCNT instruction. It is amazing how competitive the Hacker’s Delight formulation is with the POPCNT instruction itself - a testament to how well modern superscalar microarchitectures can run diverse code.
If the Hacker’s Delight version of popcount excites you, check out the code from the book here, and also check out the Stanford bit twiddling hacks, both of which show many other ways to implement popcount.
For those unfamiliar with assembly syntax “immediates” are constant operands specified in the instruction stream as opposed to a register or memory location.
According to Sean Eron Anderson’s epic bit twiddling hacks page, the transformation is widely attributed to Brian Kernighan due to its presence in an exercise in The C Programming Language, but per Knuth, Peter Wegner first published it in Communications of the ACM 3 (1960), p 322.



It's amazing how modern compilers and superscalar CPUs can take crappy code and still make it run fast. That is a hilarious way to vectorize a loop.