k'th Largest Element

Or, how to ruin a l33tcode interview question

One difficulty I have with interview coding questions is that they sometimes haunt me for long periods of time after the interview. On the bright side, every once in a while I come up with solutions that are beyond anything the interviewer might have imagined when they asked the question. And usually, that’s an opportunity to learn, even if it didn’t help get me the job. The coverage of iterative Merge Sort in my second book, for example, stemmed from a Microsoft interview round (c. 1991) where every single interview question was a whiteboard coding question asking that I reformulate recursive algorithms in iterative form.

In one such case, an interviewer asked me to write a function that returned the third-highest value in an array. For candidates familiar with the C++ STL, it may be tempting to invoke the C++ STL function nth_element() that does just this:

std::nth_element( v.begin(), v.begin()+v.size()-3, v.end() );

The problem is that nth_element() appears to wrap an implementation of Quickselect, the cousin to Quicksort that runs in expected-linear time because it only recurses on one of the two subarrays after the partitioning step. Quickselect, though fast (not optimal – like Quicksort, it suffers from O(N²) worst-case runtime), is terrible for modern CPUs because of the type of unpredictable memory traffic it triggers: data-dependent, conditional swaps of array elements. Modern CPUs hate nothing more than permuting array elements, especially if they can be in far-flung parts of memory, sparsely referencing different cache lines! Availability of data is the limiting reagent of all compute these days, so using 64B cache lines (the x86 standard) to swap 4B elements is exceptionally wasteful. In this context, any reuse within the cache is somewhat coincidental.

Happily, when asked this third-largest question, I wrote a function that kept the top three values in registers, and updated them with a decision tree on each loop iteration. I believe this met the interviewer’s goal of filtering out candidates for the type of performance engineering role I was interviewing for: Such an algorithm scans the input array, rather than trying to rearrange it, and enlists hardware prefetchers when they are available and, as a result, runs much faster.

int32_t
thirdLargest( const std::vector<int32_t>& v )
{
    int32_t v0, v1, v2;

    auto swap_if = []( int32_t& x, int32_t& y, bool predicate ) -> void {
        if ( predicate ) {
            std::swap( x, y );
        }
    };

    auto insertNewMax = [&v0, &v1, &v2, swap_if]( int32_t v3 ) -> void {
        v0 = v3;
        swap_if( v0, v1, v0>v1 );
        swap_if( v1, v2, v1>v2 );
    };
    {
        v0 = v[0];
        v1 = v[1];
        v2 = v[2];

        swap_if( v0, v2, v0>v2 );
        swap_if( v0, v1, v0>v1 );
        swap_if( v1, v2, v1>v2 );
    }

    for ( size_t i = 3; i < v.size(); ++i ) {
        if ( v[i] > v0 ) {
            insertNewMax( v[i] );
        }
    }
    return v0;
}

On my laptop, this function runs 3-11x faster than nth_element(), with an average speedup of 7.4x and standard deviation of 2.8.

As an aside, I tested using the Hacker’s Delight formulation of swap_if, and it ran at exactly the same speed as the more ergonomic code shown above. Using a template parameter fancySwap to enable the branchless, logical-op intensive conditional swap, that code would look like this:

auto swap_if = []( int32_t& x, int32_t& y, bool predicate ) -> void {
    if ( fancySwap ) {
        int32_t mask = -int32_t(predicate);
        x ^= y;
        y ^= (x&mask);
        x ^= y;
    }
    else {
        if ( predicate ) std::swap( x, y );
    }
};

We can thank the architects of modern CPUs for making the easy-to-write, easy-to-understand version just as fast. You can’t blame me for trying, though! I am old enough to remember when a taken branch was 16 clocks versus 4 clocks for a branch not taken. The code is still in the sample, in case you want to run your own tests.

What About Larger k?

I don’t recall my interviewer doing this, but the obvious escalation once a successful solution to the Third-Largest problem has been implemented is to ask: What about the k’th largest value, for arbitrary values of k? What if we want to know, say, the 100^th largest value in the array instead of the 3^rd-largest? We still have nth_element(), of course, but we also can replace our 3 explicit values with an array maxSoFar of size k, and keep them sorted in increasing order. Any incoming value larger than maxSoFar[0], the “minimum maximum” if you will, will cause maxSoFar[0] to be replaced and the incoming value then must be placed in the correct sorted order in the array. This operation amounts to the insertion step in the bedrock Insertion Sort algorithm, which may be asymptotically slow, but is still an important and useful algorithm. Let’s see what our algorithm looks like with a maxSoFar array of size k instead of our explicit 3 values:

template<uint32_t k>
int32_t
kthLargest_sort( const std::vector<int32_t>& v )
{
    // Local array we keep sorted in increasing order
    // The first element is smallest, so any incoming element
    // that is larger must be replace that element, then get
    // moved into position
    std::array<int32_t,k> maxSoFar;

    for ( size_t i = 0; i < k; i++ ) {
        maxSoFar[i] = v[i];
    }
    std::sort( maxSoFar.begin(), maxSoFar.end() );
    int32_t minMax = maxSoFar[0];
    for ( size_t i = k; i < v.size(); i++ ) {
        int32_t x = v[i];

        if ( minMax < x ) {
            size_t j;
            for ( j = 1; j < k && maxSoFar[j] < x; j++ ) {
                maxSoFar[j-1] = maxSoFar[j];
            }
            maxSoFar[j-1] = x;
            minMax = maxSoFar[0];
        }
    }
    return maxSoFar[0];
}

Since maxSoFar is small and local to the stack, shifting its elements around doesn’t have the cache line problem we alluded to earlier – even for large k, it exhibits very cache-friendly behavior. But the number of operations performed for each input element grows linearly with k. At some point, for sufficiently large k, nth_element() likely will run faster. We’ll get into more detail in the Performance Analysis section, but I was surprised at how big k (and maxSoFar) could get before performance stopped being competitive with the STL’s nth_element().

Enter Binary Heaps

Do we need to keep the elements sorted? If you intuition says No, your intuition is correct! For small k, the question makes little difference, but for larger k, there’s a known data structure – the binary heap – that can hold the k largest elements found in the array so far, but the heap only takes O(lgk) time to update, because it does not maintain the elements in sorted order.

My first introduction to binary heaps was in Programming Pearls by Jon Bentley (c. 1986)¹. Although heaps conceptually include nodes with parents and children, they are defined to be complete binary trees (no missing children), so can be densely packed into arrays. A clever indexing scheme, not pointers, is used to navigate between parent and child nodes in the heap. When using zero-based indexing, the index of the parent of the i’th heap element is (i-1)/2, and its children are 2i+1 and 2i+2. For a heap to be valid, the values of each child node must be greater than or equal to its parent.

Here's an example heap of size 6, which is represented in memory simply as

{1, 3, 5, 7, 9, 11}

          1
       /     \
      3       5
     / \     /
    7   9  11

To “heapify” an array, we call an operation SiftUp on each array element in turn. SiftUp checks to see if a given element is “smaller” than its parent and, if so, swaps with the parent, working its way toward the “top” of the heap (element zero. The algorithm can early-out: SiftUp stops comparing and swapping as soon as it sees that a node’s parent is less than the node value.

template<typename T, std::size_t k>
inline void
SiftUp( std::array<T,k>& x, size_t i )
{
    while ( i ) {
        size_t p = (i-1)>>1;
        if ( x[p] < x[i] )
            break;
        std::swap( x[i], x[p] );
        i = p;
    }
}

For our application, we are not heapifying the entire array; we are creating a heap of size k, to hold the k largest elements found so far in the input array. Once our k-sized heap is created, the first element with index 0 is known to be the smallest value in the heap; so it is at once:

• the value that must be compared with incoming array elements, to see if they belong in the heap, and

• the value that must be replaced as soon as such an array element is identified.

Once that first element has been replaced, the heap property may no longer hold true, so we perform an operation called SiftDown() that moves downward in the heap, swapping each element with the smaller of its two children until the heap property holds again.

template<typename T, std::size_t k>
inline void
SiftDown( std::array<T,k>& x, size_t i=0 )
{
    size_t c;
    while ( (c = i+i+1) < k ) {
        if ( (c+1)<k && (x[c+1]<x[c]) )
            c += 1;
        if ( x[i] < x[c] ) break;
        std::swap( x[i], x[c] );
        i = c;
    }
}

Here, SiftDown takes the place of the Insertion Sort step, but instead of performing O(k) operations to make the array sorted again, we SiftDown to perform O(lgk) make the heap property hold again. For larger k, SiftDown() should be much faster than the insertion step (e.g. for k=1000, up to 10 swaps instead of up to 1,000 insertion steps).

Now that the basic operations of creating and updating the heap are defined, we can implement our algorithm for any k. Each update of the heap takes O(lgk) steps, and for small k, the heap stays local in very fast L1 cache for the CPU.

The code we’re using in this article to build and update the heap, is from my second book, Classical Algorithms in C++ (c. 1995). My treatment of binary heaps relied heavily on Jon Bentley’s coverage of binary heaps in his Programming Pearls. The only change to the code shown here is that I’ve templatized the heap size as well as the array element type.

Using SiftUp() to build our k-element heap and SiftDown() to update it when necessary, the kthLargest() function may be implemented as follows:

template<uint32_t k>
int32_t
kthLargest_heap( const std::vector<int32_t>& v )
{
    std::array<int32_t,k> heap;

    for ( size_t i = 0; i < k; i++ ) {
        heap[i] = v[i];
        SiftUp( heap, i );
    }
    int32_t minMax = heap[0];
    for ( size_t i = k; i < v.size(); i++ ) {
        int32_t x = v[i];

        if ( minMax < x ) {
            heap[0] = x;
            SiftDown( heap );
            minMax = heap[0];
        }
    }
    return heap[0];
}

Performance Analysis

Before we delve into the tradeoffs between the different algorithms described above, let’s observe that it’s difficult to implement one whose performance is independent of the input.

For example, if the first k values are, in fact, the largest in the input array, then all of our algorithms will quickly scan through the remaining input, rejecting candidates until the end of the input array is reached. From the CPU’s perspective, that becomes a performance test for its hardware prefetchers and branch prediction.

On the opposite end of the spectrum, if the array is sorted, then every input element will trigger a rearrangement of the maxSoFar array (whether an Insertion Sort step or a SiftDown of the heap), echoing the worst-case performance of Quicksort, where naïve implementations run in O(N²) on already-sorted inputs.

The bulk of our performance analysis will be done across 10 randomized input arrays of size 100*2²⁰, but we’ll also gather best- and worst-case performance numbers to confirm our suspicions about how they will behave on sorted inputs.

For nth_element(), the algorithm ran at the same speed for all k, about 37M elements per second. It’s by far the slowest option, so we’ll take it as the baseline and report the speedups of the different formulations.

For the k’th largest, we only have the kthLargest_sort() and kthLargest_heap() variants, which feature expected runtime of O(Nk) and O(Nlgk), respectively. Algorithmic analysis would dictate that nth_element(), the Quickselect implementation in the STL, will run faster than kthLargest_sort() for some k. How big does k have to get before our cache-friendlier kthLargest_sort() gets overtaken by its inferior algorithmic complexity?

In a similar vein, we know that kthLargest_heap() has better algorithmic complexity than kthLargest_sort(), so can ask the same question: where is the crossover? For k==1000, lgk is 10. Shuffling elements up to 1,000 times seems like it would take a lot longer than comparing and swapping elements up to 10 times. But as we already know from our foray into the Hacker’s Delight formulation of a conditional swap, modern CPUs can surprise us and the only way to find out for sure is with real-world testing.

The test program for this article times the kth-largest algorithms with varying values of k: 100…1000, 1000…10,000, and 10,000-100,000. (I may have just spoiled the findings)

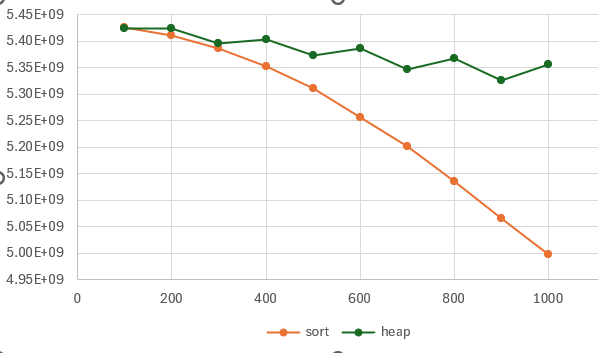
For k<=1,000, only slight differences in performance are noted:

      Units: 100M's of elements/s

  k    sort   heap  % faster
 100   5.43   5.42  0%
 200   5.41   5.42  0%
 300   5.39   5.40  0%
 400   5.35   5.40  1%
 500   5.31   5.37  1%
 600   5.26   5.39  2%
 700   5.20   5.35  3%
 800   5.14   5.37  5%
 900   5.07   5.33  5%
1000   5.00   5.36  7%

Amazingly, maintaining a sorted array of the 1,000 largest elements in the input array only runs 7% slower than maintaining a heap. (Both formulations are about 15x faster than nth_element().) The trend is more clear if we chart it, though; Substack has lame support for tables and charts, and Excel’s heuristics for choosing scales and offsets amount to a flair for the dramatic, but you can see where this is going:

It’s interesting, but I have not investigated, why the heap implementation seesaws back and forth for ‘odd’ values (k=600 is slightly faster than k=500, for example).

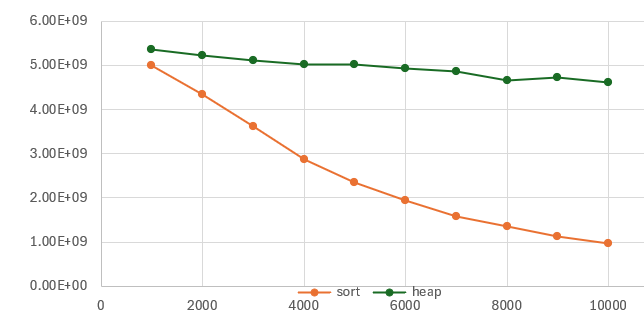
Let’s see how sort’s performance disadvantage changes if we increase k some more:

  k     sort   heap  % faster
 1000   5.00   5.36  7%
 2000   4.35   5.22  20%
 3000   3.61   5.10  41%
 4000   2.88   5.03  75%
 5000   2.36   5.02  113%
 6000   1.95   4.94  153%
 7000   1.58   4.87  208%
 8000   1.35   4.66  246%
 9000   1.12   4.72  320%
10000   0.97   4.62  378%

For k=10000, the heap is 4.78x faster, and the performance disparity continues to diverge.

The final question on my mind was what value of k would cause kthLargest_sort() to be even slower than the STL’s nth_element(), and on this CPU at least, the answer is somewhere between k=10,000 and k=20,000. (Much larger than I would have expected.)

What’s Next? SIMD, of course

This is the Parallel Programmer Substack, after all.

So far, we’ve explored the design space that a good coder might be able to explore during a coding interview. We’ve been good computer science students and used our algorithm analysis skills, replacing an expected-O(N) algorithm with bad cache behavior with an O(Nk) algorithm with an O(Nlgk) algorithm. But what if we give ourselves permission to revisit the sorting algorithm, with the help of SIMD? Can the insertion step for Insertion Sort be implemented in O(1) time on a small array?

Yes. Yes, it can. But an exploration of how will have to wait until the next article.

1. Bentley just called them “heaps,” but even for my 1995 book, I adopted the term “binary heap” to disambiguate from the heaps used by memory allocators.